Sólidos en revolución- Método de discos y arandelas
Sólidos en revolución-Método de discos:
2. Este método consiste en hacer rotar nuestra función sobre algún eje para obtener un sólido de revolución que pueda modelarse como la sumatoria de discos. El área transversal de los discos será el área de un circulo  , y el ancho será un
, y el ancho será un  . Es importante saber el eje de rotación, ya que dependiendo de esto se encuentra o despeja la ecuación en función de la variable específicamente. Por ejemplo si rotáramos la función en el eje y, despejamos la función dependiendo de y. Siendo el ancho del disco
. Es importante saber el eje de rotación, ya que dependiendo de esto se encuentra o despeja la ecuación en función de la variable específicamente. Por ejemplo si rotáramos la función en el eje y, despejamos la función dependiendo de y. Siendo el ancho del disco  . También f(x) = r.
. También f(x) = r.


2.Introducción
En este tema revisarás otra aplicación importante de la integral definida para calcular el volumen de un sólido tridimensional a partir del método de discos.
¿Sabías que los sólidos de revolución (volumen) los puedes generar al hacer girar una región plana alrededor de un eje? Por ejemplo, un cilindro surge al girar un rectángulo alrededor de uno de sus lados. Por lo común se utilizan sólidos de revolución en ingeniería y manufactura. Algunos ejemplos son botellas, pistones, etcétera.
Explicación
13.1 Cálculo de volumen de solidos por el método de discos
Al rotar una región en el plano alrededor de una recta, generas un sólido de revolución y la recta se llama eje de revolución.
Volumen del disco = (área de disco) (anchura de disco)![]()

El método del disco se aplica para determinar el volumen de un sólido de revolución. Este método requiere encontrar la suma de los volúmenes de discos representativos para aproximar el volumen del sólido. Cuando se incrementa el número de discos la aproximación es más exacta. Este mismo procedimiento fue el que utilizaste para encontrar el área bajo una curva y lo seguirás aplicando; es el concepto de la integral definida.
Método de los discos:
Para encontrar el volumen de un sólido de revolución aplicando el método de los discos utilizarás una de las fórmulas siguientes:
Eje de revolución horizontal | Eje de revolución vertical |
Volumen =
Si la anchura del rectángulo es | Volumen =
Si la anchura del rectángulo es |
3.
5. https://calculo2mp.wordpress.com/volumen-solido-de-revolucion/
https://a14121-32067953.cluster211.canvas-user-content.com/courses/14121~140/files/14121~32067953/course%20files/ma/ma13005/bb/tema13.htm
Solidos en revolucion: Metodo de arandelas
Si la región que se hace girar para generar el sólido de revolución no se acerca al eje de rotación, ni está en él, tendremos que al girarlo sobre el eje se obtendrá un agujero en su centro, es decir, un sólido de revolución con un agujero alrededor del eje de rotación. Si utilizamos el mismo método visto anteriormente para calcular su volumen, en vez de discos, tendremos que las secciones transversales perpendiculares al eje de rotación son arandelas, el área de la arandela está dada como:
Donde
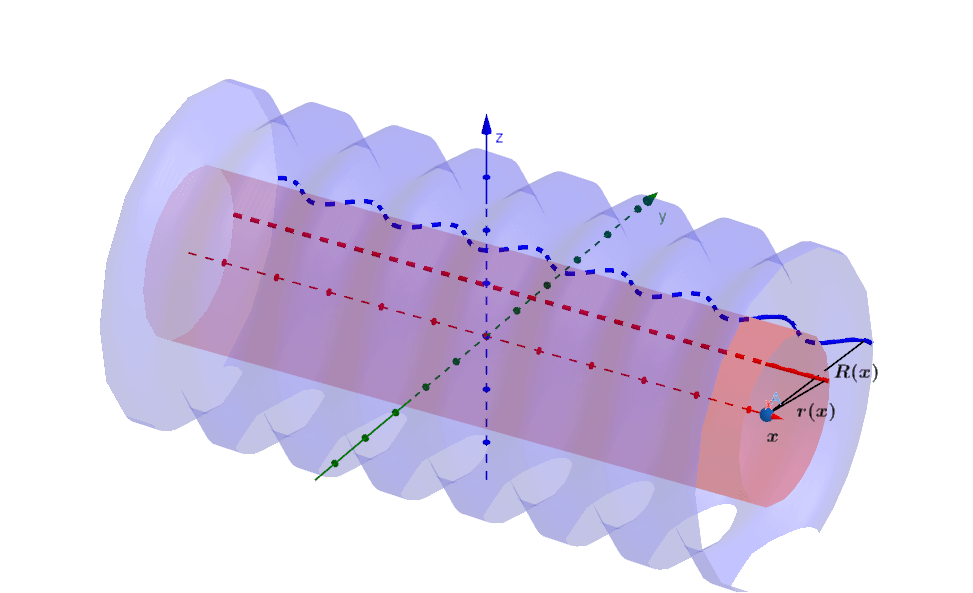
 o
o  dependiendo del eje de rotación.
dependiendo del eje de rotación.
Método de ARANDELAS
El método de Arandelas o Washer, es una extensión del método de discos para sólidos huecos. Donde se tiene un radio interno r y un radio R externo de la arandela.

La integral que contiene el radio interno representa el volumen del hueco y se resta de la integral que contiene el radio externo.


3.
4.
5. https://calculo2mp.wordpress.com/volumen-solido-de-revolucion/








Comentarios
Publicar un comentario