UNIDAD II, CLASE I -DERIVADAS
DERIVADAS
- Es la tasa de cambio de una función en un punto específico.
- La explicación de la derivada como una función es que refleja la tasa de cambio de una variable respecto a otra.
- La interpretación geométrica de la derivada es la pendiente de la recta tangente a un punto de la función
Un sencillo ejemplo es el siguiente. Imagina que hay una función que calcula la posición de un coche en el tiempo. La derivada de esta función, nos indicará a qué velocidad va el coche en cada momento.
Derivada de una función: Explicación sencilla
Desde una perspectiva geométrica, la derivada de una función es la pendiente de la recta tangente al punto donde se ubica x.
En términos matemáticos, la derivada de una función puede expresarse de la siguiente forma:
En la fórmula, x es el punto en el que la variable toma el valor de x. Asimismo, h es cualquier número. Este luego se igualará a cero pues, como vemos en la imagen superior, debemos calcular el límite de la función cuando h se acerca a cero.
Cabe recordar que, en general, la derivada es una función matemática que se define como la tasa de cambio de una variable respecto a otra. Es decir, en qué porcentaje aumenta o disminuye una variable cuando otra también se ha incrementado o disminuido.
Debemos precisar que el límite de una función se define como la tendencia de esta (a qué valor se aproxima) cuando uno de sus parámetros (en este caso h) se acerca a un valor determinado.
Derivada de una función
Así como ahora fue posible decir (a partir de lo anteriormente discutido) que la derivada de una función representa la recta tangente a una curva y es una herramienta que permite evaluar la forma en que se presenta el cambio en una función, será fácil entender e incluso intuir el procedimiento para obtenerla.
Este método se denomina método de los cuatro pasos para obtener la derivada de una función, y consiste en sistematizar el procedimiento realizado anteriormente.
Método de los cuatro pasos
Dada una función “f(x)” (como dijo Newton, el problema fundamental es obtenerla), su derivada se obtiene al seguir los cuatro pasos que se detallan a continuación. Pulsa las flechas para avanzar y retroceder por la información.
1. Evaluar la función para un incremento de la variable independiente (∆x), esto es:
f(x + ∆x) (3.1)
A continuación, se presenta un breve ejemplo para consolidar el aprendizaje del procedimiento enunciado.
Ejemplo 1. Un nuevo producto de una empresa tiene un comportamiento comercial obtenido a partir de los reportes de las ventas desde su fecha de lanzamiento, de acuerdo con la siguiente función matemática:
f(x) = x2 - 2x + 2 (e1); la variable “x” representa el tiempo y “f(x)” la venta de productos. |
Obtener el comportamiento de las ventas mensuales asociadas para el primero, segundo y tercer mes.
Solución
Como ya sabes, se debe partir de la función que describe las ventas; para resolver el planteamiento, se aplica el concepto de derivada a través de la obtención de su ecuación por el método de los cuatro pasos. Pulsa las flechas para avanzar y retroceder por la información.
De esta manera se llega a la ecuación (e1p4), la cual permite evaluar el cambio de las ventas del nuevo producto y decidir su viabilidad comercial. Si se realiza esto para cada mes (x=1, x=2 y x=3), se obtiene:
a) x=1; 2x – 2: 2(1) -2 = 0
b) x=2; 2x – 2: 2(2) -2 = 2
c) x=3; 2x – 2: 2(3) -2 = 4
Para obtener las ordenadas de los valores en que esto sucede, se sustituyen los valores de la variable “x” en la ecuación original (e1), y se obtiene la ordenada correspondiente:
y(x) = x2 - 2x + 2
x = 1; y(1) = (1)2 - 2(1) + 2 = 1; (1,1)
x = 2; y(2) = (2)2 - 2(2) + 2 = 2; (2,2)
x = 3; y(3) = (3)2 - 2(3) + 2 = 5; (3,5)
Esto se ilustra a continuación:
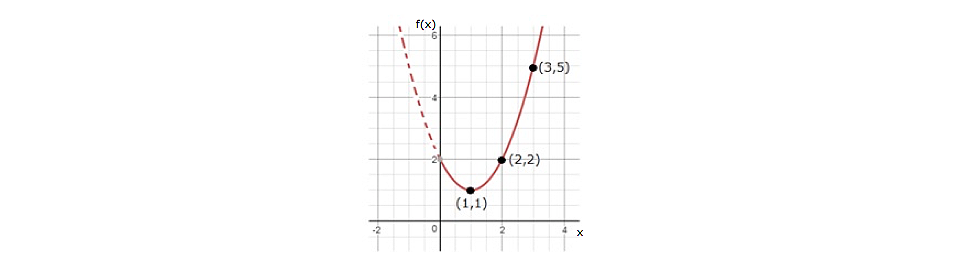
Las coordenadas correspondientes a los meses “x” evaluados
Así es como se obtienen los resultados solicitados. A continuación, observarás lo que se debe hacer con ellos.
3.



Comentarios
Publicar un comentario